| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 투 포인터
- 민주주의
- 알고리즘
- Python
- 내란수괴
- 다익스트라
- 유니온 파인드
- 윤석열
- dfs
- 재귀함수
- 윤석열 내란수괴
- 내란수괴 윤석열
- LCA
- ccw
- 파비우스 전략
- union find
- 내란죄
- dfs 백트래킹
- DP
- 오블완
- 이분 탐색
- 프림
- 구조론
- BFS
- 분할정복
- 백준
- 비상계엄
- Prim
- 티스토리챌린지
- 왈왈왈
- Today
- Total
Toolofv 님의 블로그
[Python] 백준 11049 - 행렬 곱셈 순서 본문
백준 - 11049 행렬 곱셈 순서
첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다. 둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500) 항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
www.acmicpc.net

문제
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.
- AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
- BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.
입력
첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.
둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)
항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.
출력
첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같다.
필요한 도구
1. DP or 재귀함수
2. PyPy3
3. 행렬의 곱셈 방식
문제 해결 방법 - (서칭으로 참고후 해결)
[Python] 백준 - 11066 파일 합치기
문제소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완
toolofv.tistory.com
위 문제와 알고리즘은 같다.
1. 행렬의 곱셈 시 A x B = X라면 X의 행과 열은 다음과 같다.
1) 아래 그림을 보면 2x2행렬과 2x2행렬의 곱은 2x2행렬이 되고, 2x3행렬과 3x2행렬을 곱했을 때, 2x2행렬이 되는 것을 알 수 있다.
각 곱셈연산의 갯수는 8번(2x2x2), 12번(2x3x2)이다.
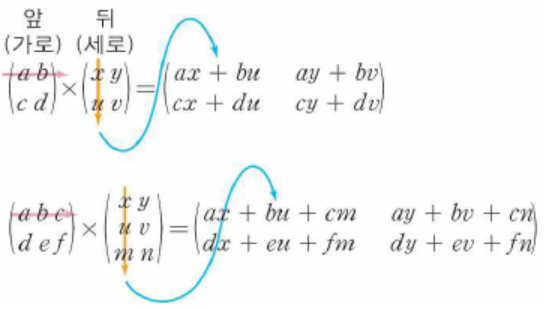
2) 11066번 문제 - 파일 합치기처럼 주어진 행렬이 만약 A, B, C일 때, 곱해지는 순서에 따라 곱셈연산의 횟수가 달라지고, 최소값을 DP에 간격이 가까운 순부터 반영해나가는 방법을 떠올릴 수 있다.
2. for문이나 재귀함수(분할정복)의 방법이 있다. 간격에 따라 종합비용이 달라지는 경우 최소값, 최대값을 구할 수 있다.
ex)
sol(0, 2) -> sol(0, 0)=0 + sol(1, 2) + M(x)
-> sol(0, 1) + sol(2, 2)=0 + M(x) ∵ 2가지 경우 중 최소값이 DP 저장
※ sol(1, 2) -> sol(1, 1)=0 + sol(2, 2)=0 + M(x) sol(0, 1) -> sol(0, 0)= 0 + sol(1, 1)=0 + M(x)
1) 분할정복의 경우, 재귀함수를 따라가 보면 행렬 리스트의 인덱스 l, r 이 l == r 이 될 때까지 깊어진다.
2) sol(1, 2)의 경우, 다음 호출 재귀함수는 모두 l == r 이 되어 0을 출력하고, M(x)는 행렬1과 행렬2의 곱셈연산값이어야 한다.
그리고 sol(0, 2)의 경우, 2가지 경우 중 최소값이 DP에 반영되고, 간격이 커질 때 마다, 경우의 수들에서 최소값이 반영되어야 한다.
점차 간격에 따라 DP에 반영되어 나간다는 걸 알 수 있다.
3) M(x)는 행렬의 곱연산 횟수의 누적합이다.
sol(1, 2)이면 M(x) = 3 x 2 x 6 , sol(0, 1)이면 M(x) = 5 x 3 x 2 이 된다.
sol(0, 2)는 위 간격1의 sol(0, 1)의 M(x) + 계산된 행렬(5 x 2) 와 남은 행렬(2 x 6)의 곱셈연산횟수가 누적된다.
계산된 행렬(5 x 2)의 경우, 그 전 재귀함수에서 M(x)의 양 끝값 (5 x 2)가 녹아있다는 걸 알 수 있다.
이 걸 토대로 M(x)의 식을 뽑아낼 수 있다.
a. (AB)C 일 때, 5×2×6 -> A[0] x B[1] x C[1] --> sol(0, 1) + sol(2, 2) + l[0] x i[1] x r[1], i = 1
b. A(BC) 일 때, 5×3×6 -> A[0] x A[1] x C[1] --> sol(0, 0) + sol(1, 2) + l[0] x i[1] x r[1], i = 0
사실 이 방법은 귀납적 시도라 행렬의 개수가 많을 경우 맞는다는 보장이 없을 수도 있어, 적어도 4~5개의 행렬이 있을 때를 확인해야 한다. 연역적인 한 줄에 꿰는 방법은 행렬을 좀 더 공부해봐야 할 것같다.
- 분할정복 재귀함수
import sys
input = sys.stdin.readline
n = int(input())
matrix = [list(map(int, input().split())) for _ in range(n)]
dp = [[0 for _ in range(n)] for _ in range(n)]
def sol(l, r):
if dp[l][r] != 0:
return dp[l][r]
if l == r:
return 0
if l+1 == r:
return matrix[l][0] * matrix[l][1] * matrix[r][1]
ans = sys.maxsize
for i in range(l, r):
A = sol(l, i)
B = sol(i+1, r)
MX = matrix[l][0] * matrix[i][1] * matrix[r][1]
ans = min(ans, A + B + MX)
dp[l][r] = ans
return dp[l][r]
print(sol(0, n-1))
- for문
import sys
input = sys.stdin.readline
n = int(input())
matrix = [list(map(int, input().split())) for _ in range(n)]
dp = [[0 for _ in range(n)] for _ in range(n)]
for distance in range(1, n): # 간격 1 2
for l in range(n-distance): # l 01 0 dp[l][r]의 l
r = l + distance # r 12 2 dp[l][r]의 r
ans = sys.maxsize
for i in range(l, r):
A = dp[l][i]
B = dp[i+1][r]
MX = matrix[l][0] * matrix[i][1] * matrix[r][1]
ans = min(ans, A + B + MX)
dp[l][r] = ans
print(dp[0][n-1])'Algorithm' 카테고리의 다른 글
| [Python] 백준 - 1260 DFS와 BFS (2) | 2024.06.11 |
|---|---|
| [Python] 백준 - 3015 오아시스 재결합 (1) | 2024.06.07 |
| [Python] 백준 2293 - 동전 1 (1) | 2024.06.05 |
| [Python] 백준 2629 - 양팔저울 (0) | 2024.06.05 |
| [Python] 백준 1520 - 내리막길 (0) | 2024.06.05 |




