| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 다익스트라
- 백준
- 구조론
- 프림
- 유니온 파인드
- 이분 탐색
- 내란죄
- DP
- 윤석열 내란수괴
- 내란수괴 윤석열
- 파비우스 전략
- dfs 백트래킹
- union find
- Prim
- 내란수괴
- 알고리즘
- 비상계엄
- ccw
- dfs
- 티스토리챌린지
- 왈왈왈
- 오블완
- 윤석열
- 재귀함수
- BFS
- 투 포인터
- 분할정복
- Python
- 민주주의
- LCA
- Today
- Total
Toolofv 님의 블로그
[Python] 백준 - 11444 피보나치 수 6 본문
백준 - 11444 피보나치 수 6
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다. n=17일때 까지 피보나치 수를 써보면 다음과 같다.
www.acmicpc.net

문제
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다.
이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가 된다.
n=17일때 까지 피보나치 수를 써보면 다음과 같다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 n번째 피보나치 수를 1,000,000,007으로 나눈 나머지를 출력한다.
피보나치 수열
1. 피보나치 수열은 수식으로는 복잡한 내용이 있는 것 같은데, 일단 앞 두 항을 계속해서 더해나가는 수열이라고 생각하자.

2. 코드로 피보나치 수열을 구하는 방법에는 여러 가지가 있는데, 이 문제는 입력으로 들어오는 수가 굉장히 크다. 반복문, 재귀함수, 메모이제이션 등의 방법(적어도 $O(n)$이다.)으로는 시간이 오래 걸린다.
1) 반복문 - $O(n)$
def fibo(n):
a, b = 0, 1
i = 0
while i < n:
a, b = b, a+b
i += 1
return a
2) 재귀함수 + 메모이제이션 - $O(n)$ (재귀함수만 사용했을 때는 중복계산이 많아, $O(2^n)$이다.)
memo = {}
def fibo(n):
if n == 0 or n == 1:
return n
if n not in memo:
memo[n] = fibo(n-2) + fibo(n-1)
return memo[n]
3) DP - $O(n)$
def fibo(n):
dp = [0, 1] + [0] * (n-1)
for i in range(2, n+1):
dp[i] = dp[i-2]+dp[i-1]
return dp
print(fibo(10))
4) 앞서의 문제 행렬 제곱과 거듭제곱(분할정복)을 활용할 수 있다. - $O(logN)$
[Python] 백준 - 10830 행렬 제곱
문제 크기가 N*N인 행렬 A가 주어진다. 이때, A의 B제곱을 구하는 프로그램을 작성하시오. 수가 매우 커질 수 있으니, A^B의 각 원소를 1,000으로 나눈 나머지를 출력한다. 입력 첫째 줄에 행렬의 크
toolofv.tistory.com
- 행렬 제곱, 거듭제곱에 대한 문제 포스팅
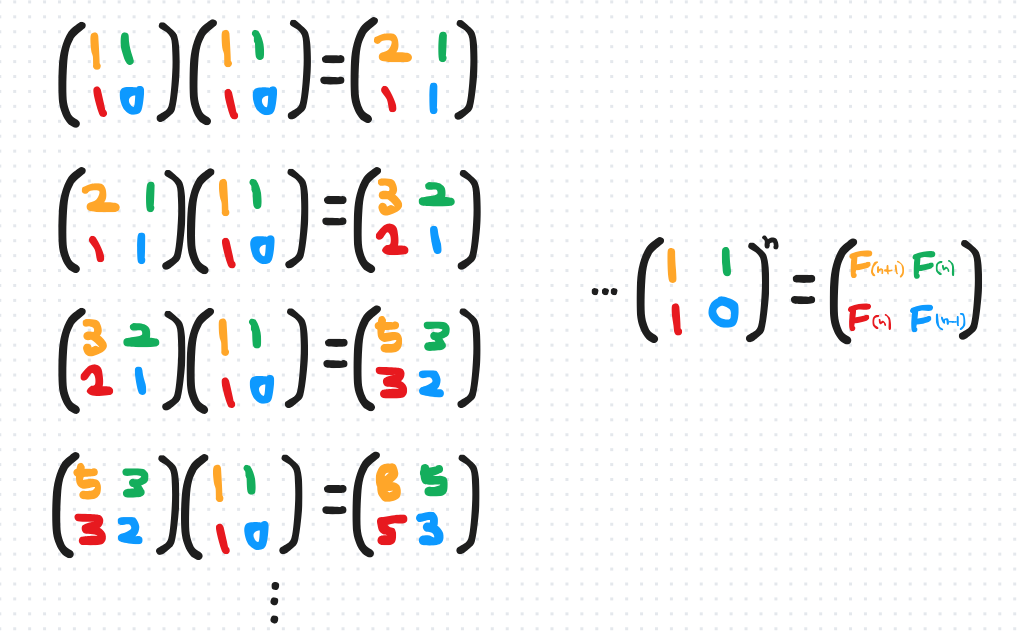
행렬 $\begin{pmatrix} 1 & 1 \\ 1 & 0 \\ \end{pmatrix}$ 을 계속 제곱하면 위 그림처럼 피보나치 수열이 구해진다. (2 x 2)행렬을 계속 곱하는 게 공간을 낭비하는 게 아닌가 싶었는데, 필요한 값만 남겨 구현하게 되면 DP로 구현하는 것과 다를 바가 없고, 오히려 공간이 더 필요하게 된다. 거듭제곱(분할정복)만을 활용해서 하는 방법도 있을 것 같긴 하다.
3. 결국 위 행렬 제곱, 거듭제곱(분할정복)의 문제와 같다. - $O(logN)$
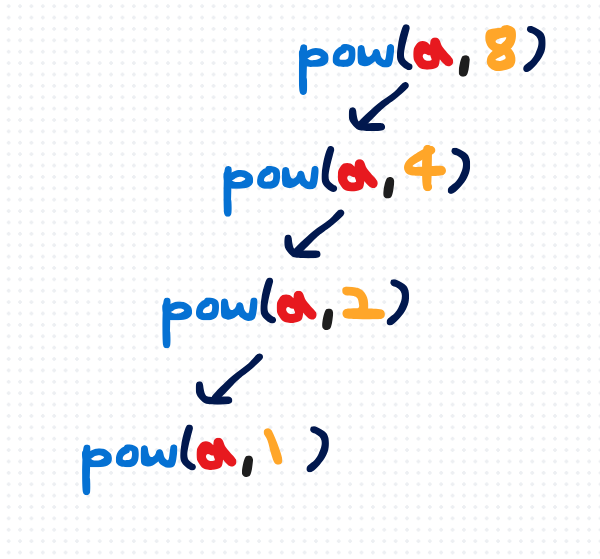
- 코드
import sys
input = sys.stdin.readline
n = int(input())
d = [[1, 1], [1, 0]]
p = 1000000007
def mul(a, b):
res = [[0 for _ in range(2)] for _ in range(2)]
for i in range(2):
for j in range(2):
t = 0
for k in range(2):
t += a[i][k]*b[k][j]
res[i][j] = t % p
return res
def pow(a, b):
if b == 1:
return a
else:
temp = pow(a, b//2)
if b % 2 == 0:
return mul(temp, temp)
else:
return mul(mul(temp, temp), a)
print(pow(d, n)[1][0])'Algorithm' 카테고리의 다른 글
| [Python] 백준 - 10816 숫자 카드 2 (이분 탐색) (0) | 2024.11.05 |
|---|---|
| [Python] 백준 - 11660 구간 합 구하기 5 (2차원 누적합) (0) | 2024.11.03 |
| [Python] 백준 - 10830 행렬 제곱 (0) | 2024.10.31 |
| [Python] 백준 - 2740 행렬 곱셈 (2) | 2024.10.30 |
| [Python] 백준 - 11401 이항 계수 3 (0) | 2024.10.29 |




