Toolofv 님의 블로그
[Python] 힙 정렬(Heap Sort) 본문
힙(Heap) 정렬 알고리즘은 정렬의 용도로 주로 쓰인다고 볼 수는 없는 것 같다. 힙 자료구조는 원소가 들어갈 때 최댓값, 최소값을 꺼내쓰는데 효율적이기 때문에 다익스트라(dijkstra) 알고리즘같은 경우에도 사용된다. 시간복잡도는 $O(n\ log\ n)$이다. 완전이진트리(complete binary tree)다. 파이썬의 경우 heapq 모듈을 사용한다.
힙 자료구조화와 정렬은 좀 다르다.
Siftdown( )의 경우 범위를 받고 부모노드(parent)를 지정한다. 바로 밑의 자식 노드를 child로 지정한 후 오른쪽의 자식 노드와 비교해 큰 값을 최종 child로 정한다. 지정된 부모노드와 자식 노드를 비교하고 자식 노드 값이 크면 바꿔준다.(최대힙의 경우) 그 것을 반복하면 부모노드와 자식 노드간에는 대소 관계를 정할 수 있다. 힙 자료구조화하는 과정에서 정렬이 완벽하게 된다고는 볼 수 없다.
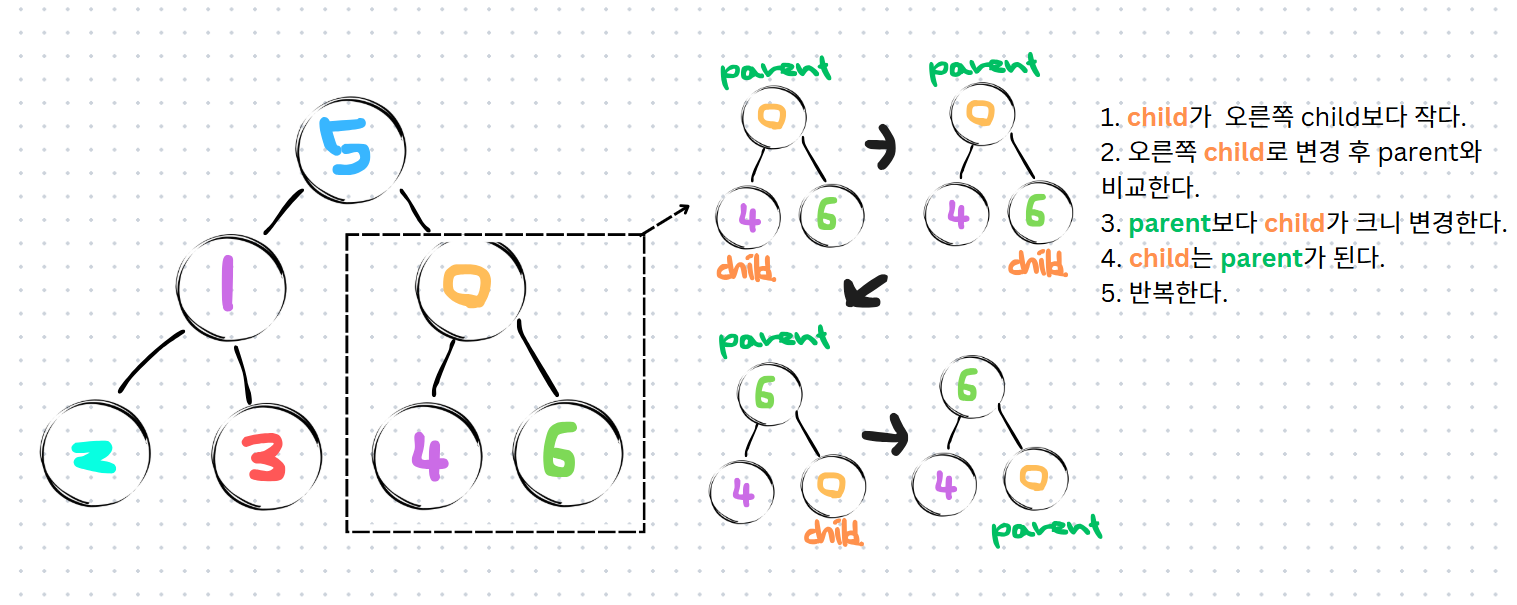
정렬할 때
트리의 루트노드는 최댓값 혹은 최소값이기에 그 것을 끝 인덱스로 보낸다. 그러면 맨 끝자리는 정렬이 완료된 셈이다. 맨 끝자리만 제외하고 힙을 다시 구성한다. 그 다음 아까와 같이 최댓값을 끝으로 보낸다. (실제로는 끝의 바로 전, 리스트 범위를 줄였기 때문) 반복하면 정렬이 완료된다.
파이썬 heapq 모듈 함수
import heapq # heapq 모듈 임포트.(최소힙이 기본)
heap = []
heapq.heappush(heap, item) # item을 heap에 추가한다.
heapq.heappop(heap) # heap에서 가장 작은 항목을 제거한다.
heapq.heappushpop(heap, item) # heap에 item을 추가하고 가장 작은 항목 제거
heapq.heapify(list) # 리스트를 힙구조로 변환한다.
heapq.heapreplace(heap, item) # heap의 최소 항목을 제거하고 item으로 대체한다.
heapq.nlargest(n, iterable, key=None) # n개의 가장 큰 항목 반환, key는 정렬기준 함수
heapq.nsmallest(n, iterable, key=None) # n개의 가장 작은 항목 반환, key는 정렬기준 함수
최대 힙을 사용해야할 경우에는 음수를 이용해 구성하고 꺼내쓰면서 양수로 바꿔주면 된다.
-코드
import sys
input = sys.stdin.readline
arr = [5, 1, 0, 2, 4, 3, 6]
def heap_sort(d):
def hsort(d):
for start in range((len(d)-2//2), -1, -1): # 막내부모노드부터 최대힙화
siftdown(d, start, len(d)-1)
for end in range(len(d)-1, 0, -1):
d[end], d[0] = d[0], d[end] # 루트노드 최댓값을 맨 끝자리 이동
siftdown(d, 0, end-1) # 맨 끝자리는 최댓값확정정, 제외하고 siftdown
return d
def siftdown(d, s, e):
parent = s # s를 부모노드 지정
while True:
child = 2 * parent + 1 # 왼쪽 자식노드
if child > e: # child가 e보다 커지면 break
break
if child + 1 <= e and d[child] < d[child+1]:
child += 1 # 범위 안에 있으면서 우측자식노드가 크면 우측으로 child변경
if child <= e and d[parent] < d[child]: # 부모노드보다 크면 바꾸고
d[parent], d[child] = d[child], d[parent]
parent = child # parent에 child인덱스반영
else:
break
return d
return hsort(d)
print(heap_sort(arr))
import sys
input = sys.stdin.readline
arr = [5, 7, 1, 9, 0, 2, 8, 4, 3, 6]
def heapify(d):
for start in range(len(d)-2//2, -1, -1):
siftdown(d, start, len(d)-1)
return d
def siftdown(d, s, e):
p = s
while True:
c = 2*p+1
if c > e:
break
if c+1 <= e and d[c] < d[c+1]:
c += 1
if c <= e and d[c] > d[p]:
d[c], d[p] = d[p], d[c]
p = c
else:
break
return d
def heap_sort(d):
heapify(d)
for end in range(len(d)-1, 0, -1):
d[end], d[0] = d[0], d[end]
siftdown(d, 0, end-1)
return d
print(heap_sort(arr))
파이썬 heapq 모듈 사용한 정렬
import sys
import heapq
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
d = [1, 6, 8, 2, 9, 3, 7, 5, 4]
def heap_sort(d):
heap = []
for i in range(len(d)):
heapq.heappush(heap, d[i])
ans = []
while heap:
ans.append(heapq.heappop(heap))
return ans
print(heap_sort(d))
[Python] 퀵 정렬(Quick Sort)
퀵 정렬(Quick Sort)은 병합 정렬(Merge Sort)와 비슷하게 분할정복(Divide and Conqueror)의 방법으로 정렬되는 알고리즘이다. 퀵 정렬은 시간복잡도로는 복불복이다. 최선, 평균의 경우 $O(n\ log\ n)$이지만
toolofv.tistory.com
[Python] 병합 정렬(Merge Sort)
정렬 알고리즘은 사실 실제로 구현해서 사용할 일은 없는 것 같다. 매일 잊어먹기 때문에 기록의 용도로 올린다. 병합 정렬(Merge Sort)의 시간복잡도는 최악의 경우부터 최선의 경우 모두 $O(n\ log\
toolofv.tistory.com
'Algorithm' 카테고리의 다른 글
| [Python] 퀵 정렬(Quick Sort) (0) | 2025.01.31 |
|---|---|
| [Python] 병합 정렬(Merge Sort) (1) | 2025.01.30 |
| [Python] 백준 - 2583 영역 구하기 (0) | 2025.01.26 |
| [Python] 백준 - 2573 빙산 (1) | 2024.12.27 |
| [Python] 백준 - 10026 적록색약 (0) | 2024.12.10 |





