| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- dfs 백트래킹
- 투 포인터
- union find
- dfs
- 유니온 파인드
- 분할정복
- ccw
- 알고리즘
- Prim
- 백준
- 티스토리챌린지
- 재귀함수
- 파비우스 전략
- 이분 탐색
- BFS
- 윤석열 내란수괴
- 비상계엄
- 내란수괴
- 다익스트라
- LCA
- 민주주의
- 구조론
- 윤석열
- 내란수괴 윤석열
- 오블완
- 왈왈왈
- DP
- Python
- 프림
- 내란죄
- Today
- Total
Toolofv 님의 블로그
[Python] 백준 - 2482 색상환 본문
백준 - 2482 색상환
입력 파일의 첫째 줄에 색상환에 포함된 색의 개수를 나타내는 양의 정수 N(4 ≤ N ≤ 1,000)이 주어지고, 둘째 줄에 N색상환에서 선택할 색의 개수 K(1 ≤ K ≤ N)가 주어진다.
www.acmicpc.net

문제
색을 표현하는 기본 요소를 이용하여 표시할 수 있는 모든 색 중에서 대표적인 색을 고리 모양으로 연결하여 나타낸 것을 색상환이라고 한다. 미국의 화가 먼셀(Munsell)이 교육용으로 고안한 20색상환이 널리 알려져 있다. 아래 그림은 먼셀의 20색상환을 보여준다.
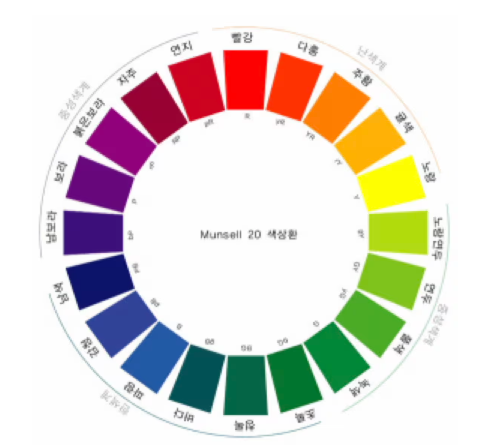
그림 1. 먼셀의 20색상환
색상환에서 인접한 두 색은 비슷하여 언뜻 보면 구별하기 어렵다. 위 그림의 20색상환에서 다홍은 빨강과 인접하고 또 주황과도 인접하다. 풀색은 연두, 녹색과 인접하다. 시각적 대비 효과를 얻기 위하여 인접한 두 색을 동시에 사용하지 않기로 한다.
주어진 색상환에서 시각적 대비 효과를 얻기 위하여 서로 이웃하지 않은 색들을 선택하는 경우의 수를 생각해 보자. 먼셀의 20색상환에서 시각적 대비 효과를 얻을 수 있게 10개의 색을 선택하는 경우의 수는 2이지만, 시각적 대비 효과를 얻을 수 있게 11개 이상의 색을 선택할 수 없으므로 이 경우의 수는 0이다.
주어진 정수 N과 K에 대하여, N개의 색으로 구성되어 있는 색상환 (N색상환)에서 어떤 인접한 두 색도 동시에 선택하지 않으면서 서로 다른 K개의 색을 선택하는 경우의 수를 구하는 프로그램을 작성하시오.
입력
입력 파일의 첫째 줄에 색상환에 포함된 색의 개수를 나타내는 양의 정수 N(4 ≤ N ≤ 1,000)이 주어지고, 둘째 줄에 N색상환에서 선택할 색의 개수 K(1 ≤ K ≤ N)가 주어진다.
출력
첫째 줄에 N색상환에서 어떤 인접한 두 색도 동시에 선택하지 않고 K개의 색을 고를 수 있는 경우의 수를 1,000,000,003 (10억 3) 으로 나눈 나머지를 출력한다.
필요한 도구
1. DP = [[0~k개 선택할 때 구성할 수 있는 경우의 수] 원형테이블에 색의 개수]
문제해결방법
※ 참고한 포스트 - 이해가 쉽고, 사고의 흐름이 돋보인다. (기하학적으로 접근)
[알고리즘][4][백준_2482][Python3] - 색상환
문제이해 문제에서는 다채로운 색이 등장하지만 단순하게 n등분 되어있는 원에서 인접하지않게 k개를 색칠하는 경우의 수를 구하는 문제이다. 알고리즘 전략 알고리즘 구현을 위한 첫걸음은 노
source-sc.tistory.com
1. 점화식이 있을 것이다.
2. n과 k를 최소나 최대로 가정해보자. 이 경우는 최소일 때부터 접근하는 게 맞아보인다.
조건
1) n개의 색이 있을 때, k = 0으로 어떠한 선택도 하지 않으면 인접을 따질 필요가 없고, 그 경우의 수는 1이다.
(dp[i][0])
2) n개의 색이 있을 때, k = 1이면(한 색만 선택하면) 인접을 따질 필요가 없고, 그 경우의 수는 n이다. (dp[i][1])
3) 문제를 푼 후, 곰곰이 생각해보면 중요한 부분인데, 위 문제에 기술되어 있는 것처럼 k > n/2이면 선택할 수 있는 경우의 수는 없다.
1) k = 2로 k를 최소화해서 생각했을 때, 딸려나오는 정보는 아래와 같다.
a. n = 3일 때까지는 색을 2가지 지정할 수가 없다. (return 0)
b. n = 4일 때, 색을 2가지 지정하는 경우의 수는 2이다.
c. n = 5일 때, 색을 2가지 지정하는 경우의 수는 5이다.
2) 어느 정도 구한 후, 표로 보면 다음과 같다.
| 색 \ 총 색개수 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| k = 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| k = 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| k = 2 | 0 | 0 | 0 | 2 | 5 | 9 | 14 |
이 표를 보면 점화식을 떠올릴 수 있을 것이다. 확장해 생각해보면, dp[i][j] = dp[i-1][j] + dp[i-2][j-1] 과 같다.
3) k > n/2의 조건이 없을 경우 dp[3][2]가 1이 되는데(return 1), 이러면 DP가 꼬인다. (원형테이블이 아니라 선형 테이블의 경우를 구한 것이 된다. 그래서 마지막 경우에서 보정을 해줘야 하는 것으로 보인다.)
- 코드
1) 재귀함수
import sys
input = sys.stdin.readline
n = int(input())
k = int(input())
dp = [[0 for _ in range(k+1)] for _ in range(n+1)]
for i in range(n+1):
dp[i][0] = 1
dp[i][1] = i
def sol(n, k):
if k > n/2:
return 0
if dp[n][k]:
return dp[n][k]
else:
A = sol(n-1, k)
B = sol(n-2, k-1)
dp[n][k] = A + B
return dp[n][k]
print(sol(n, k) % 1000000003)
2) for
import sys
input = sys.stdin.readline
n = int(input())
k = int(input())
dp = [[0 for _ in range(k+1)] for _ in range(n+1)]
for i in range(n+1):
dp[i][0] = 1
dp[i][1] = i
for i in range(2, n+1):
for j in range(2, k+1):
if i/2 < j:
dp[i][j] = 0
else:
dp[i][j] = dp[i-1][j] + dp[i-2][j-1]
dp[i][j] %= 1000000003
print(dp[n][k])'Algorithm' 카테고리의 다른 글
| [Python] 백준 - 2565 전깃줄 (0) | 2024.10.15 |
|---|---|
| [Python] 백준 - 2162 선분 그룹 (0) | 2024.10.14 |
| [Python] 백준 - 17404 RGB거리 2 (0) | 2024.10.08 |
| [Python] 백준 - 2098 외판원 순회 (1) | 2024.10.04 |
| [Python] 백준 - 1904 01타일 (2) | 2024.10.01 |




