| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 내란죄
- 오블완
- 백준
- 유니온 파인드
- BFS
- 윤석열 내란수괴
- DP
- 다익스트라
- 이분 탐색
- 파비우스 전략
- 투 포인터
- 윤석열
- 민주주의
- 알고리즘
- 프림
- 비상계엄
- 구조론
- 재귀함수
- LCA
- 내란수괴 윤석열
- dfs 백트래킹
- union find
- Prim
- 티스토리챌린지
- 왈왈왈
- ccw
- Python
- 내란수괴
- dfs
- 분할정복
- Today
- Total
Toolofv 님의 블로그
[Python] 백준 - 2533 사회망서비스(SNS) 본문
백준 - 2533 사회망서비스(SNS)
첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 ≤ N ≤ 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에지 (u, v)를 나타내는 두 정수 u와 v가 하나의 빈칸을 사이에 두고 주어진다.
www.acmicpc.net

문제
페이스북, 트위터, 카카오톡과 같은 사회망 서비스(SNS)가 널리 사용됨에 따라, 사회망을 통하여 사람들이 어떻게 새로운 아이디어를 받아들이게 되는가를 이해하는 문제가 중요해졌다. 사회망에서 사람들의 친구 관계는 그래프로 표현할 수 있는데, 이 그래프에서 사람은 정점으로 표현되고, 두 정점을 잇는 에지는 두 정점으로 표현되는 두 사람이 서로 친구 관계임을 표현한다.
예를 들어, 철수와 영희, 철수와 만수, 영희와 순희가 서로 친구 관계라면 이를 표현하는 친구 관계 그래프는 다음과 같다.
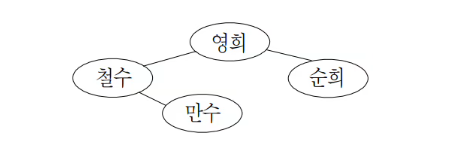
친구 관계 그래프를 이용하면 사회망 서비스에서 어떤 새로운 아이디어가 전파되는 과정을 이해하는데 도움을 줄 수 있다. 어떤 새로운 아이디어를 먼저 받아들인 사람을 얼리 아답터(early adaptor)라고 하는데, 사회망 서비스에 속한 사람들은 얼리 아답터이거나 얼리 아답터가 아니다. 얼리 아답터가 아닌 사람들은 자신의 모든 친구들이 얼리 아답터일 때만 이 아이디어를 받아들인다.
어떤 아이디어를 사회망 서비스에서 퍼뜨리고자 할 때, 가능한 한 최소의 수의 얼리 아답터를 확보하여 모든 사람이 이 아이디어를 받아들이게 하는 문제는 매우 중요하다.
일반적인 그래프에서 이 문제를 푸는 것이 매우 어렵다는 것이 알려져 있기 때문에, 친구 관계 그래프가 트리인 경우, 즉 모든 두 정점 사이에 이들을 잇는 경로가 존재하면서 사이클이 존재하지 않는 경우만 고려한다.
예를 들어, 8명의 사람으로 이루어진 다음 친구 관계 트리를 생각해보자. 2, 3, 4번 노드가 표현하는 사람들이 얼리 아답터라면, 얼리 아답터가 아닌 사람들은 자신의 모든 친구가 얼리 아답터이기 때문에 새로운 아이디어를 받아들인다.
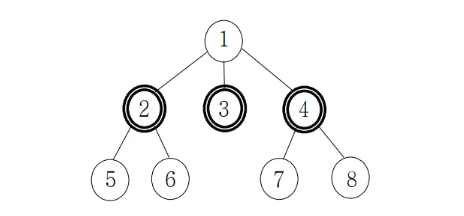
친구 관계 트리가 주어졌을 때, 모든 개인이 새로운 아이디어를 수용하기 위하여 필요한 최소 얼리 어답터의 수를 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 ≤ N ≤ 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에지 (u, v)를 나타내는 두 정수 u와 v가 하나의 빈칸을 사이에 두고 주어진다.
출력
주어진 친구 관계 그래프에서 아이디어를 전파하는데 필요한 얼리 아답터의 최소 수를 하나의 정수로 출력한다.
문제해결방법
[Python] 백준 - 2213 트리의 독립집합
문제그래프 G(V, E)에서 정점의 부분 집합 S에 속한 모든 정점쌍이 서로 인접하지 않으면 (정점쌍을 잇는 간선이 없으면) S를 독립 집합(independent set)이라고 한다. 독립 집합의 크기는 정점에 가중
toolofv.tistory.com
준비 도구
1. 주어진 트리 그래프
2. DP리스트 = [선택함, 선택하지 않음] x (n+1)
3. DFS 동작의 중복을 방지하는 방문리스트
도구 사용
1. dfs알고리즘에서 재귀함수 호출하는 부분 다음에 코드를 적어준다는 것은 끝까지 재귀함수가 파고들었을 때부터 상향식으로 값이 변동할 수 있게 구현이 가능하다는 것이다.
2. 위 트리의 독립집합 문제의 경우는 아래와 같다.
dp[idx][0] += dp[next][1]
dp[idx][1] += max(dp[next][0], dp[next][1])- 트리의 독립집합
이는 idx로 표시되어있는 현재노드를 선택한다면 그 전 노드는 자연히 선택할 수 없다는 의미와
현재노드를 선택하지 않았다면 그 이전 값의 최댓값을 가져올 수 있다는 뜻이다.
dp[idx][0] += min(dp[next])
dp[idx][1] += dp[next][0]- 사회망 서비스(SNS)
이번 문제에서는 반대로 구현해야 하는데, 이는 현재 노드를 선택했다면 밑의 노드는 그 이전 값의 최소값을 가져올 수 있고, 현재노드를 선택하지 않았다면, 무조건 그 이전노드를 선택해야 한다는 의미이다. (얼리어답터는 적어도 한 칸이내에 존재해야 한다.)
- 코드
import sys
import math
from collections import deque
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def dfs(idx):
v[idx] = 1
dp[idx][0] = 1
dp[idx][1] = 0
for next in graph[idx]:
if v[next] == 0:
dfs(next)
dp[idx][0] += min(dp[next])
dp[idx][1] += dp[next][0]
n = int(input())
graph = [[] for _ in range(n+1)]
v = [0 for _ in range(n+1)]
dp = [[0, 0] for _ in range(n+1)]
for _ in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
dfs(1)
print(min(dp[1]))'Algorithm' 카테고리의 다른 글
| [Python] 백준 - 9663 N-Queen (1) | 2024.09.23 |
|---|---|
| [Python] 백준 - 25682 체스판 다시 칠하기 2 (0) | 2024.09.20 |
| [Python] 프로그래머스 - 2023 KAKAO BLIND RECRUITMENT 미로 탈출 명령어 (0) | 2024.09.10 |
| [Python] 백준 - 11866 요세푸스 문제 0 (1) | 2024.09.08 |
| [Python] 백준 - 3176 도로 네트워크 (0) | 2024.09.03 |




