| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 비상계엄
- 알고리즘
- 백준
- 분할정복
- dfs
- 이분 탐색
- 파비우스 전략
- 내란수괴 윤석열
- BFS
- Python
- 유니온 파인드
- 민주주의
- 구조론
- 윤석열 내란수괴
- ccw
- 재귀함수
- LCA
- 왈왈왈
- 윤석열
- dfs 백트래킹
- 내란수괴
- Prim
- DP
- 프림
- 다익스트라
- 내란죄
- 투 포인터
- 오블완
- 티스토리챌린지
- union find
- Today
- Total
Toolofv 님의 블로그
[Python] 백준 - 11401 이항 계수 3 본문
백준 - 11401 이항 계수 3
자연수 \(N\)과 정수 \(K\)가 주어졌을 때 이항 계수 \(\binom{N}{K}\)를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
www.acmicpc.net

문제
자연수 과 정수 가 주어졌을 때 이항 계수 를 1,000,000,007로 나눈 나머지를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 과 가 주어진다. (1 ≤ ≤ 4,000,000, 0 ≤ ≤ )
출력
를 1,000,000,007로 나눈 나머지를 출력한다.
필요한 도구
1. 페르마의 소정리
2. 모듈러 연산 분배법칙(나눗셈은 적용 X)
3. 팩토리얼 연산 (3! = 1 x 2 x 3)
4. 거듭제곱 연산(분할정복)
문제해결방법
1. 다른 이항계수 문제와 다르게 주어지는 수가 굉장히 크다. 그냥 조합을 구하고, 나머지 연산을 하는 방법으로는 시간이 오래 걸릴 것을 예상할 수 있다.
2. 조합의 경우의 수를 구하는 공식은 다음과 같다. (0 ≤ K ≤ N일 때)
(조합과 페르마의 소정리에 대한 증명, 모듈러 연산의 분배법칙은 검색을 통해 쉽게 알 수 있다.)
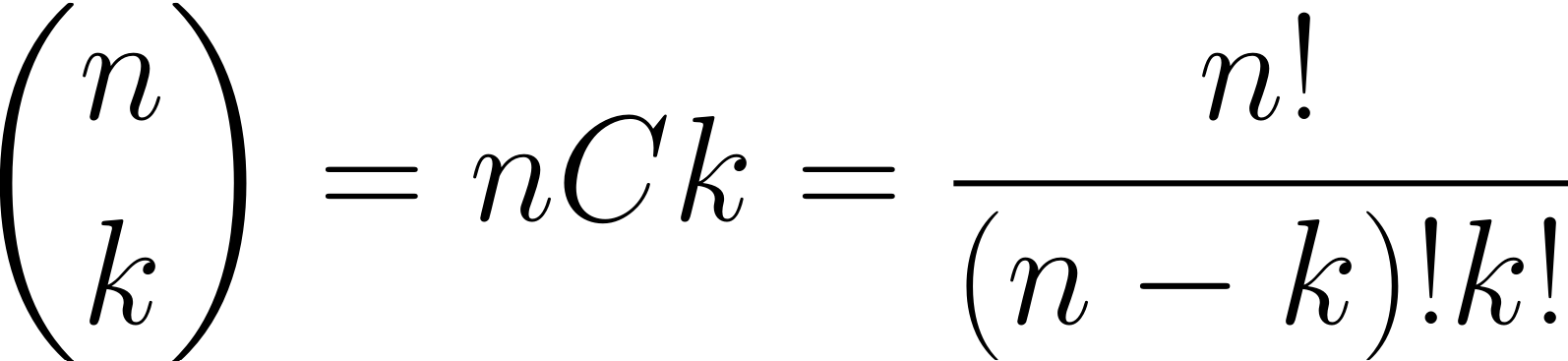
3. 모듈러 연산의 분배법칙은 나눗셈의 경우 작동하지 않는다. 나눗셈의 꼴을 곱셈으로 변환시켜준다. 여기에 페르마의 소정리가 쓰인다.
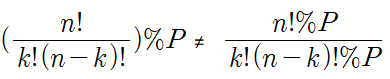
4. 페르마의 소정리에 따르면, p가 소수일 때, 아래의 식과 같이 합동이다.
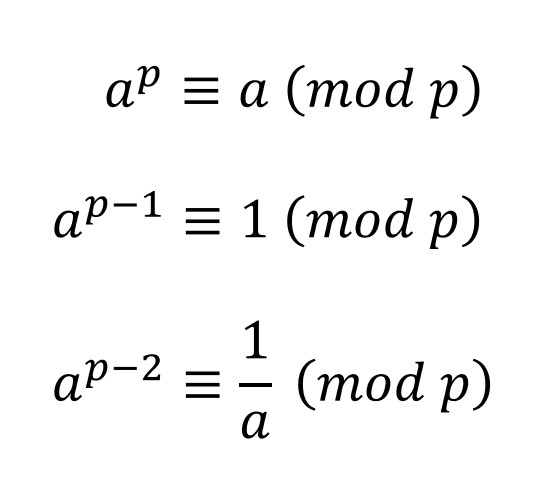
5. 조합의 분모 부분의 식을 아래와 같이 바꾸어 줄 수 있다. 그리고 합동인 아래 식과 위 조합식의 분자 부분을 곱하면 된다는 걸 알 수 있다.
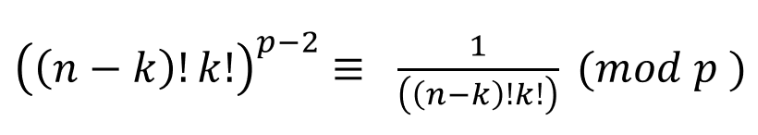
결과적으로 아래와 같은 꼴로 바꾸어 줄 수 있다.

이제 팩토리얼 함수와 큰 수일 때 효과적인 거듭제곱 함수를 이용해 코드를 작성하면 된다.
- 코드
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
p = 1000000007
def fac(int):
res = 1
for i in range(2, int+1):
res *= i
res %= p
return res
def pow(a, b):
if b == 1:
return a % p
else:
t = pow(a, b//2)
if b % 2 == 0:
return (t**2) % p
else:
return (t**2*a) % p
a = fac(n)
b = fac(n-k)*fac(k)
print(a * pow(b, p-2) % p)'Algorithm' 카테고리의 다른 글
| [Python] 백준 - 10830 행렬 제곱 (0) | 2024.10.31 |
|---|---|
| [Python] 백준 - 2740 행렬 곱셈 (2) | 2024.10.30 |
| [Python] 백준 - 10872 팩토리얼 (0) | 2024.10.28 |
| [Python] 백준 - 7562 나이트의 이동 (1) | 2024.10.23 |
| [Python] 백준 - 1707 이분 그래프 (0) | 2024.10.22 |




